<<Back

Analysis Using SAS

  Analysis Using SPSS      

For the analysis of the data SPSS steps are given in the sequel.

Data Input:

For performing analysis, input the data in the following format. 

{Here average Plant Population is termed as (PP), average Plant Height as (PH), average Number of Green Leaves as (NGL) and Yield (kg/plot) as YLD and serial number as SN. It may, however, be noted that one can retain the same name or can code in any other fashion}.

 Following are the brief description of the steps along with screen shots.

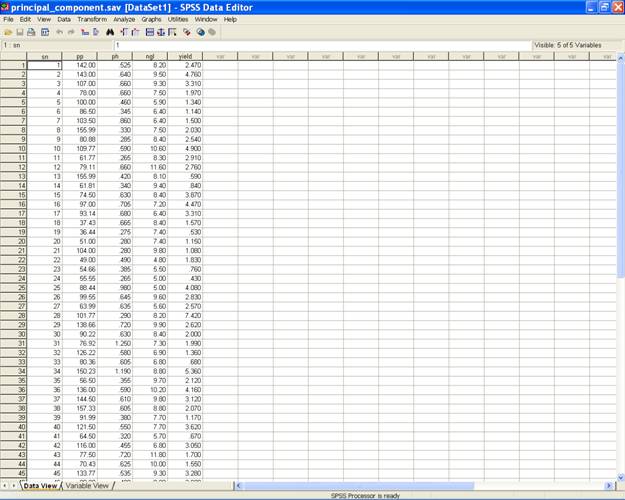
·         Enter data in SPSS Data Editor. There are two views in SPSS Data Editor. In variable view, one can define the name of variables and variable type string or numeric and data view gives the spreadsheet in which data pertaining to variables may be entered in respective columns. In the present case, we enter data in numeric format.

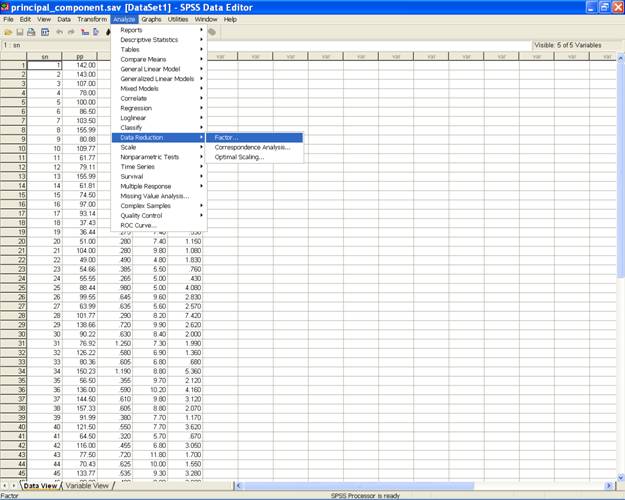
·         Choose Analyze from the Menu Bar. Now select Analyze → Data Reduction → Factor…

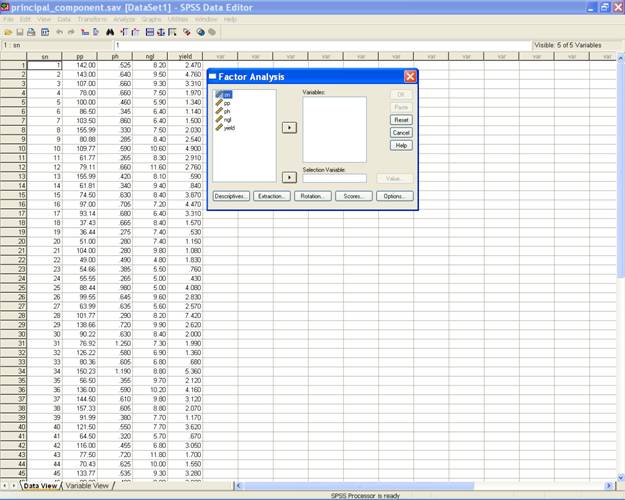
·         This selection displays the following screen.

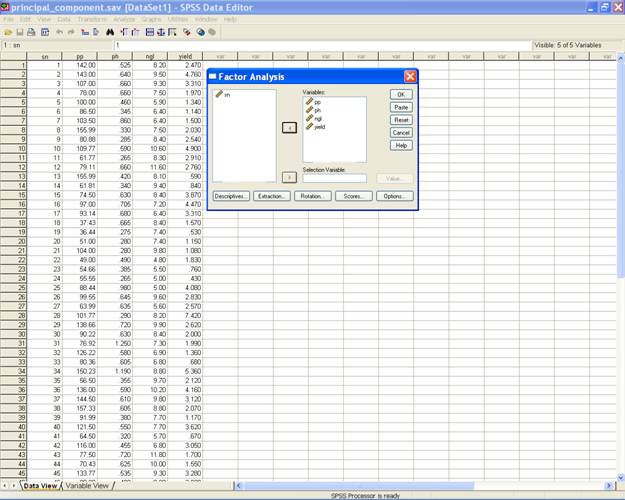
·         Select the variables pp, ph, ngl and yield to be analyzed and send them to the variables: box.

·         This displays the following screen.

·   Click on Descriptives…

·   In the Statistics area: Select Univariate descriptive and Initial solutions..

·   This displays the following screen.

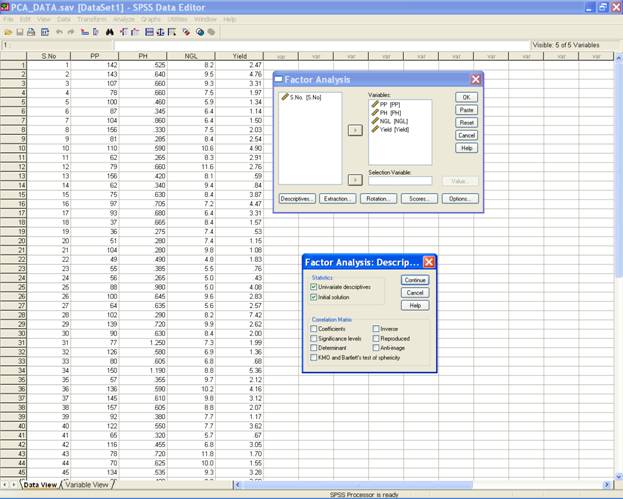
·         Click on continue to return to the Factor Analysis dialog box.

·         Click on Extraction. The Extraction dialog box will appear.

·         Method: The default is Principal Components.

·         Select Covariance matrix in the Analyze option.

·         This displays the following screen.

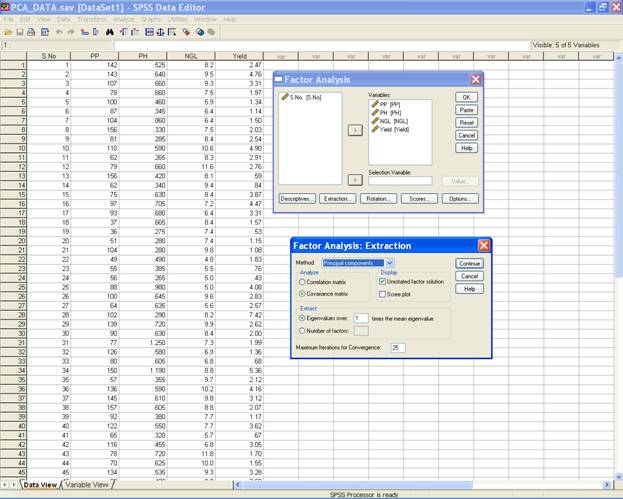
·         Click on continue to return to the Factor Analysis dialog box.

·         Click on Paste to go to the syntax editor mode.

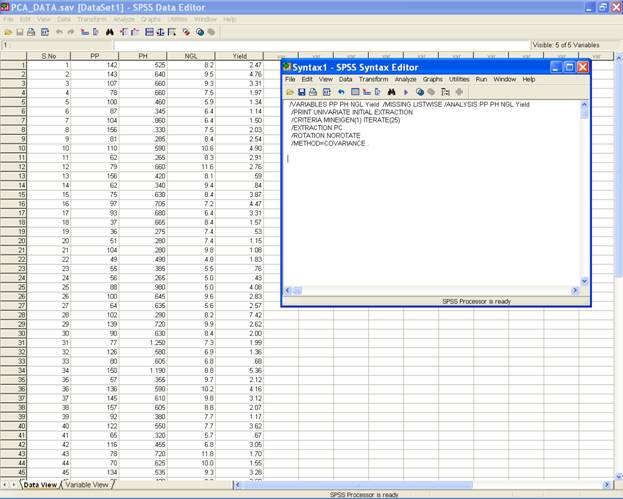
·         To compute the principal component scores from the original variables using Covariance matrix use the following syntax in the syntax editor window.

MATRIX.

GET X/VARIABLES=PP,PH,NGL,YIELD.  /*READS THE DATA INTO THE MATRIX X, DEFINE THE VARIABLES ACCORDING TO THE DATA */

COMPUTE XSSCP=SSCP(X).        /*SUM OF SQUARES AND CROSS PRODUCTS*/

COMPUTE XSUM=CSUM(X).   /*SUM OF THE VARIABLES IN THE DATA SET*/

COMPUTE N=NROW(X).    /*TOTAL NUMBER OF OBSERVATIONS*/

COMPUTE XBAR=XSUM/N.  /*MEAN OF THE VARIABLES IN THE DATA */

PRINT XBAR.

COMPUTE XX=T(XBAR)*XBAR.

COMPUTE COVMAT=(XSSCP-(N*XX))/(N-1).   /*COVARIANCE MATRIX FOR THE GIVEN DATA */

PRINT COVMAT.

CALL EIGEN(COVMAT,EIGVEC,EIGVAL). /*COMPUTES THE EIGENVALUES AND THE EIGENVECTORS FOR THE COVARIANCE MATRIX*/

PRINT EIGVAL.

PRINT EIGVEC.

COMPUTE TRANS=T(X).

COMPUTE TRANSA=T(EIGVEC).

COMPUTE SCORES=TRANSA*TRANS.

COMPUTE PCASCORE=T(SCORES).    /* COMPUTES THE PRINCIPAL COMPONENT SCORES*/

PRINT PCASCORE./TITLE "PRINCIPAL COMPONENT SCORES FROM THE ORIGINAL VARIABLES".

END MATRIX.

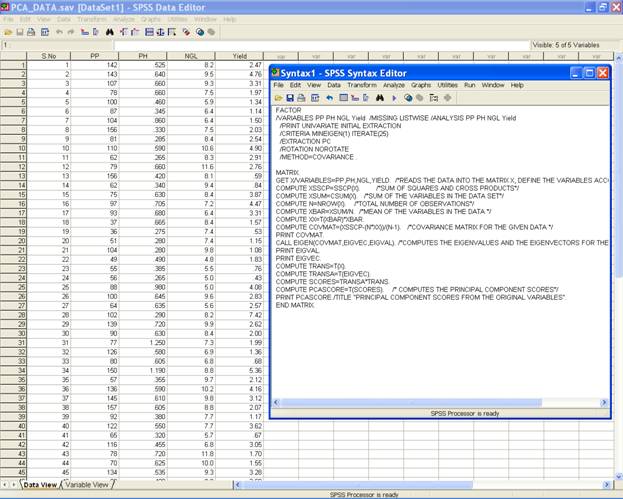
·         Click on RUN → ALL to get the principal component scores for the original variables.

One can define the following syntax in the syntax editor after creating the data file to compute the principal component scores from the original variables using covariance matrix 

FACTOR

/VARIABLES PP PH NGL Yield 

/MISSING LISTWISE

 /ANALYSIS PP PH NGL Yield

/PRINT UNIVARIATE INITIAL EXTRACTION

/CRITERIA MINEIGEN(1) ITERATE(25)

/EXTRACTION PC

/ROTATION NOROTATE

/METHOD=COVARIANCE .

MATRIX.

GET X/VARIABLES=PP,PH,NGL,YIELD. /*READS THE DATA INTO THE MATRIX X, DEFINE THE VARIABLES ACCORDING TO THE DATA */

COMPUTE XSSCP=SSCP(X). /*SUM OF SQUARES AND CROSS PRODUCTS*/

COMPUTE XSUM=CSUM(X). /*SUM OF THE VARIABLES IN THE DATA SET*/

COMPUTE N=NROW(X). /*TOTAL NUMBER OF OBSERVATIONS*/

COMPUTE XBAR=XSUM/N. /*MEAN OF THE VARIABLES IN THE DATA */

COMPUTE XX=T(XBAR)*XBAR.

COMPUTE COVMAT=(XSSCP-(N*XX))/(N-1). /*COVARIANCE MATRIX FOR THE GIVEN DATA */

PRINT COVMAT.

CALL EIGEN(COVMAT,EIGVEC,EIGVAL). /*COMPUTES THE EIGENVALUES AND THE EIGENVECTORS FOR THE COVARIANCE MATRIX*/

PRINT EIGVAL.

PRINT EIGVEC.

COMPUTE TRANS=T(X).

COMPUTE TRANSA=T(EIGVEC).

COMPUTE SCORES=TRANSA*TRANS.

COMPUTE PCASCORE=T(SCORES). /* COMPUTES THE PRINCIPAL COMPONENT SCORES*/

PRINT PCASCORE./TITLE "PRINCIPAL COMPONENT SCORES FROM THE ORIGINAL VARIABLES".

END MATRIX.

NOTE: If one wants to compute the principal component scores on the standardized data variables then use the following steps.

To compute the principal component scores from the standardized data variables using Correlation matrix use the following steps.

·         To standardize the data use the following steps.

• Choose Analyze from the Menu Bar. Now select Analyze → Descriptive Statistics → Descriptives…

·          In the Descriptives dialog box select the variables and check the option save standardized values as variables.

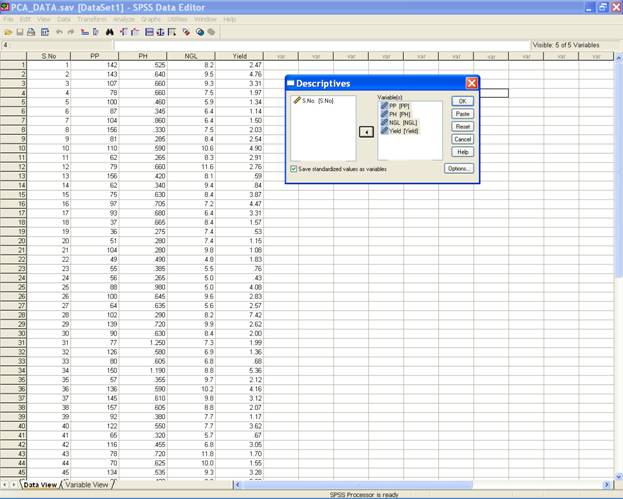
• Click on OK to get  the standardized values for the variables.

•   To perform the principal component analysis use the following steps.

   

• Choose Analyze from the Menu Bar. Now select Analyze → Data Reduction → Factor…

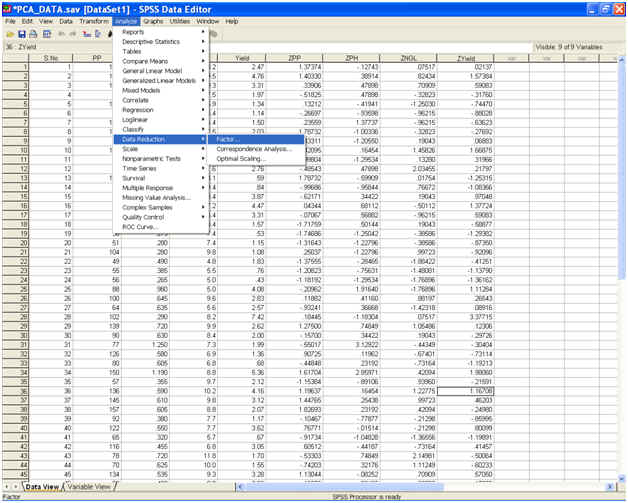
·         Select the standardized variables zpp, zph, zngl and zyield to be analyzed and send them to the variables: box.

·         This displays the following screen.

·         Click on Paste to go to the Syntax mode for the computation of the principal component scores.

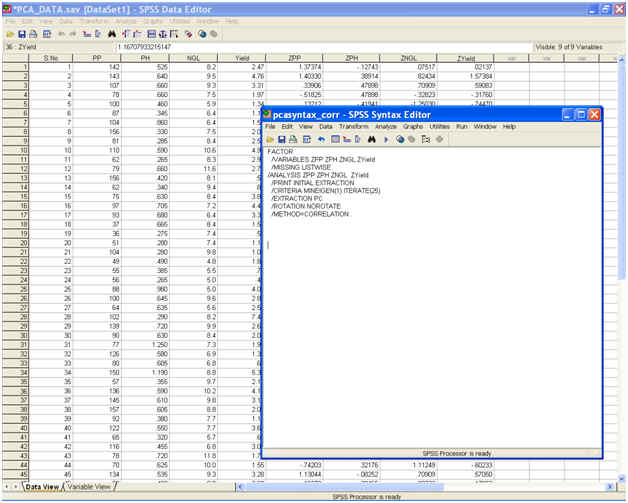
·         To compute the principal component scores from the standardized data variables using Correlation matrix type the following syntax in the syntax editor window.

MATRIX.

GET X/VARIABLES=PP,PH,NGL,YIELD.  /*READS THE DATA INTO THE MATRIX X, DEFINE THE VARIABLES ACCORDING TO THE DATA */

COMPUTE XSSCP=SSCP(X).        /*SUM OF SQUARES AND CROSS PRODUCTS*/

COMPUTE XSUM=CSUM(X).   /*SUM OF THE VARIABLES IN THE DATA SET*/

COMPUTE N=NROW(X).    /*TOTAL NUMBER OF OBSERVATIONS*/

COMPUTE XBAR=XSUM/N.  /*MEAN OF THE VARIABLES IN THE DATA */

COMPUTE XX=T(XBAR)*XBAR.

COMPUTE COVMAT=(XSSCP-(N*XX))/(N-1).   /*COVARIANCE MATRIX FOR THE GIVEN DATA */

COMPUTE D=MDIAG(SQRT(DIAG(COVMAT))).

COMPUT R=INV(D)*COVMAT*INV(D).  /*CORRELATION MATRIX FOR THE GIVEN DATA */

PRINT R.

CALL EIGEN(R,REIGVEC,REIGVAL). /*COMPUTES THE EIGENVALUES AND THE EIGENVECTORS FOR THE COVARIANCE MATRIX*/

PRINT REIGVAL.

PRINT REIGVEC.

GET SX/VARIABLES=ZPP,ZPH,ZNGL,ZYIELD.  /*READS THE STANDARIZED DATA INTO THE MATRIX SX. DEFINE THE VARIABLES ACCORDING TO THE DATA */

COMPUTE TRANSS=T(SX).

COMPUTE TRANSAS=T(REIGVEC).

COMPUTE SCORESS=TRANSAS*TRANSS.

COMPUTE PCASCORES=T(SCORESS).    /* COMPUTES THE PRINCIPAL COMPONENT SCORES*/

PRINT PCASCORES./TITLE "PRINCIPAL COMPONENT SCORES FROM THE STANDARDIZED VARIABLES".

END MATRIX.

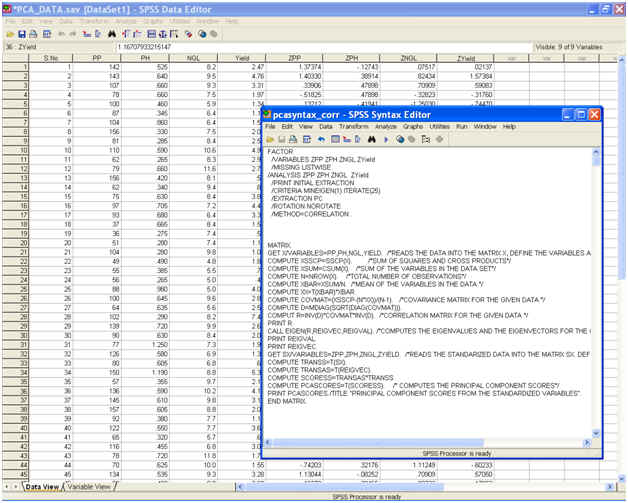
·         Click on RUN → ALL to get the principal component scores from the standardized data variables.

 One can define the following syntax in the syntax editor after creating the data file to compute the principal component scores from the  standardized variables using correlation matrix.

DESCRIPTIVES

VARIABLES=PP PH NGL Yield /SAVE.

FACTOR

/VARIABLES ZPP ZPH ZNGL ZYield

/MISSING LISTWISE

/ANALYSIS ZPP ZPH ZNGL ZYield

/PRINT INITIAL EXTRACTION

/CRITERIA MINEIGEN(1) ITERATE(25)

/EXTRACTION PC

/ROTATION NOROTATE

/METHOD=CORRELATION .

MATRIX.

GET X/VARIABLES=PP,PH,NGL,YIELD. /*READS THE DATA INTO THE MATRIX X, DEFINE THE VARIABLES ACCORDING TO THE DATA */

COMPUTE XSSCP=SSCP(X). /*SUM OF SQUARES AND CROSS PRODUCTS*/

COMPUTE XSUM=CSUM(X). /*SUM OF THE VARIABLES IN THE DATA SET*/

COMPUTE N=NROW(X). /*TOTAL NUMBER OF OBSERVATIONS*/

COMPUTE XBAR=XSUM/N. /*MEAN OF THE VARIABLES IN THE DATA */

COMPUTE XX=T(XBAR)*XBAR.

COMPUTE COVMAT=(XSSCP-(N*XX))/(N-1). /*COVARIANCE MATRIX FOR THE GIVEN DATA */

COMPUTE D=MDIAG(SQRT(DIAG(COVMAT))).

COMPUT R=INV(D)*COVMAT*INV(D). /*CORRELATION MATRIX FOR THE GIVEN DATA */

PRINT R.

CALL EIGEN(R,REIGVEC,REIGVAL). /*COMPUTES THE EIGENVALUES AND THE EIGENVECTORS FOR THE COVARIANCE MATRIX*/

PRINT REIGVAL.

PRINT REIGVEC.

GET SX/VARIABLES=ZPP,ZPH,ZNGL,ZYIELD. /*READS THE STANDARIZED DATA INTO THE MATRIX SX. DEFINE THE VARIABLES ACCORDING TO THE DATA */

COMPUTE TRANSS=T(SX).

COMPUTE TRANSAS=T(REIGVEC).

COMPUTE SCORESS=TRANSAS*TRANSS.

COMPUTE PCASCORES=T(SCORESS). /* COMPUTES THE PRINCIPAL COMPONENT SCORES*/

PRINT PCASCORES./TITLE "PRINCIPAL COMPONENT SCORES FROM THE STANDARDIZED VARIABLES".

END MATRIX.

Home Descriptive Statistics  Tests of Significance Correlation and Regression Completely Randomised Design  RCB Design  

Incomplete Block Design  Resolvable Block Design  Augmented Design  Latin Square Design Factorial RCB Design  

Partially Confounded Design Factorial Experiment with Extra Treatments Split Plot Design Strip Plot Design 

Response Surface Design Cross Over Design  Analysis of Covariance Diagnostics and Remedial Measures 

Principal Component Analysis Cluster Analysis Groups of Experiments  Non-Linear Models  

Contact Us