Analysis  Using  SPSS

To answer the question whether there is any difference between treatment and residual effects. Rearrange the data in the following order: animal numbers as units 

  alphabetical numbers as treatments

and residual effect as residual (coding could be done as follows: for every first period the number one has assigned (fixed) and for other periods  code 1 to 3 are given according to the treatment received by the unit in the previous period).

Note: A carry-over or residual term has the special property as a factor, or class variate, of having no level in the first period because the treatment in the first period is not affected by any residual or carry over effect of any treatment. When we consider the residual or carryover effect in practice the fact that carry-over or residual effects will be adjusted for period effects (by default all effects are adjusted for all others in these analysis). As a consequence, any level can be assigned to the residual variate in the first period, provided the same level is always used. An adjustment for periods then removes this part of the residual term. (For details a reference may made to Jones, B. and Kenward,M.G. 2003. Design and Analysis of Cross Over Trials. Chapman and Hall/CRC. New York . Pp: 212)

Data Input:
For performing analysis, input the data in the following format.

{Here we call animal numbers as units, periods as periods, treatment number as treat and residual effect as residual. It may, however, be noted that one can retain the same name or can code in any other fashion}. 

Main Procedure is:  

•   Open Data editor: Start→ All Programs → SPSS for Windows→ SPSS 15.0/SPSS13.0/ SPSS10.0

•  Enter data in SPSS Data editor. There are two views in SPSS Data Editor. In variable view, one can define the name of variables and variable types as string or numeric depending on the nature of the data and data  view gives the spreadsheet in which data    pertaining to variables may be entered in   respective columns.

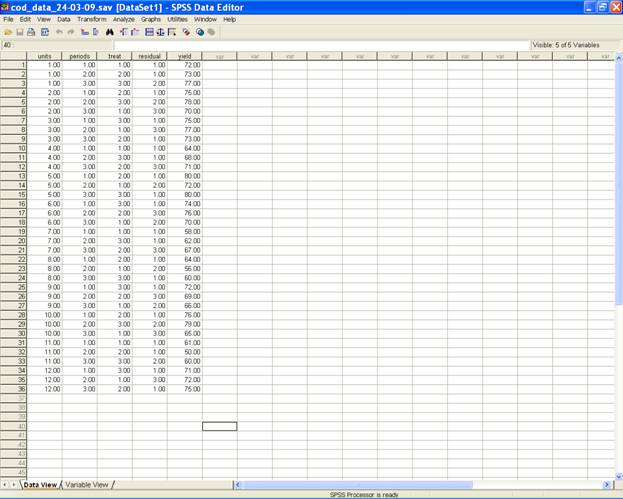
•  Once the data entry is completed, Choose Analyze from the Menu Bar. Now select

 Analyze→ General linear Model → Univariate. 

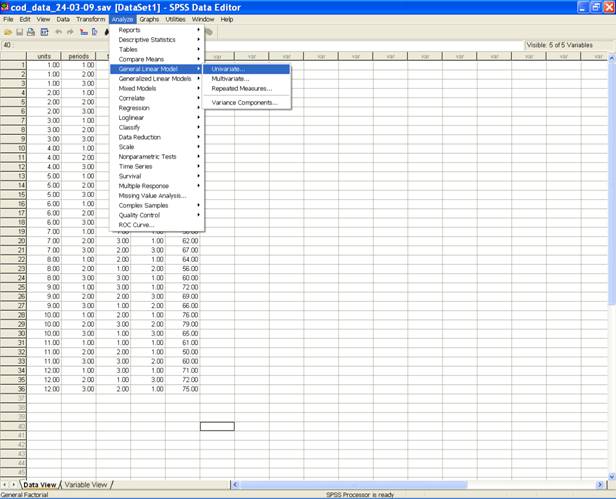
•  This selection displays the following screen

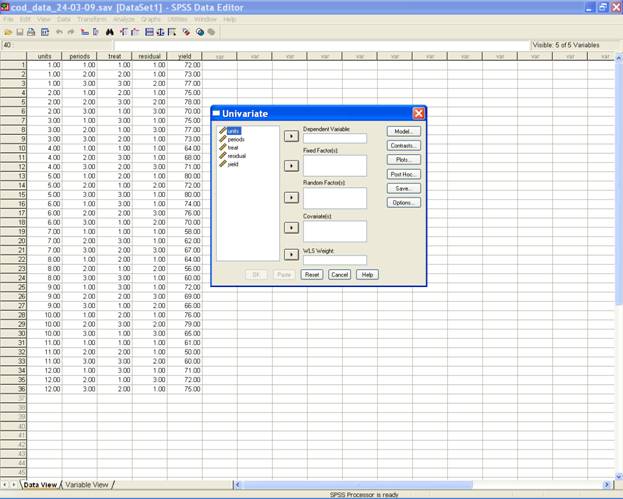
• Select yield and send it to the Dependent Variable box; units, periods, treat and residual may be selected for  Fixed Factor(s) box. After doing these the dialog box should be like this.

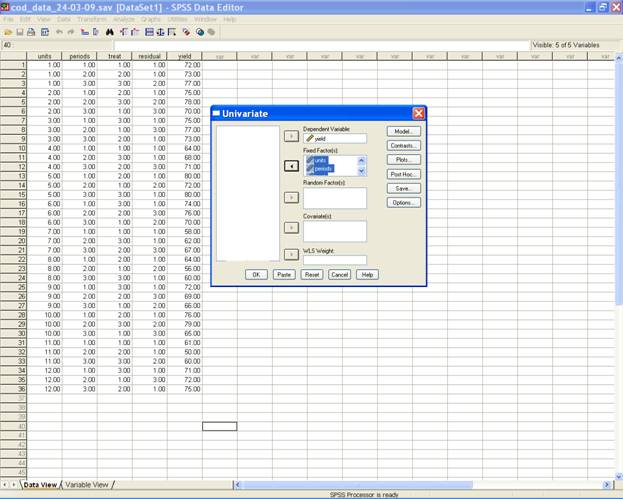
• Now define model as per design adopted to analyze the data. A Click on the model displays Univariate: Model dialog box. Click on custom then change the Build Terms as Main effects and send units, periods, treat and residual to the Model box and then select type III sum of squares.

Note: if anyone is interested on the random effect of units, they have to send the units into random factors and proceed as follows.

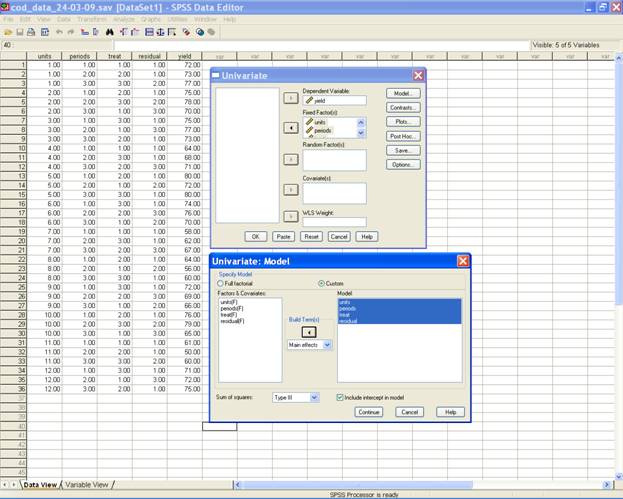
• Click Continue to return back to the Univariate dialog box, 

• Now select options to perform the all possible pairwise comparisons of direct and residual effects.

• Send treat and residual from factor(s) and factor interactions to display means for; then tick compare main effects and select LSD(none)

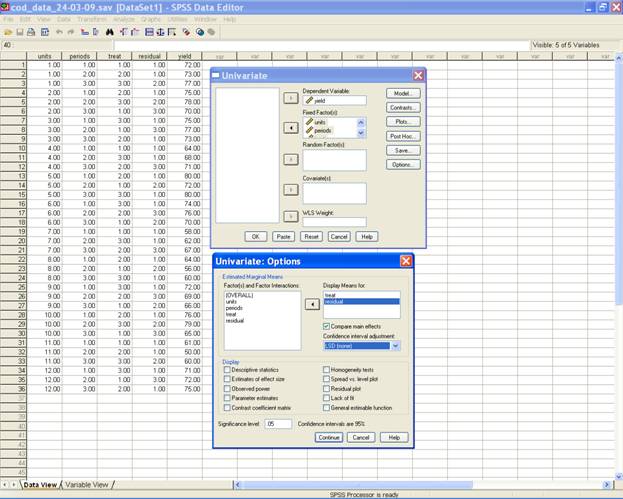
NOTE: Before clicking continue one can check the options available there in the Univariate:options by ticking the appropriate options  according to your requirements like significance level, Descriptive Statistics etc.

·         Click continue to go back to the Univariate dialog box.

·         Click ok to get the final output

Note: Type III sum of squares provide adjustment against all the effects appearing in the model. If the user is interested in getting separate ANOVA for the two cases viz. (i) adjusted treatment effects and unadjusted residual effect and (ii) unadjusted treatment effects and adjusted residual effects, all  the above steps are same except in the screen shot 6 where we have to define the univariate model in the following passion (units periods residual treat )  for (i) and (units periods treat residual) for (ii) with type I sum of squares.( keeping the order of fixed effects  is important for (i) and (ii)). 

 One can define the following syntax in the syntax editor after creating the data file to test whether there is any difference between treatment and residual effects by using type III sum of squares. 

UNIANOVA

  yield  BY units periods treat residual

  /METHOD = SSTYPE(3)

  /INTERCEPT = INCLUDE

  /EMMEANS = TABLES(treat) COMPARE ADJ(LSD)

  /EMMEANS = TABLES(residual) COMPARE ADJ(LSD)

  /CRITERIA = ALPHA(.05)

  /DESIGN = units periods treat residual .

Note: Type III sum of squares provide adjustment against all the effects appearing in the model. If the user is interested in getting separate ANOVA for the two cases viz. (i) adjusted treatment effects and unadjusted residual effect and (ii) unadjusted treatment effects and adjusted residual effects, then the above syntax can be written twice with type I sum of squares as respectively:

UNIANOVA

yield  BY units periods residual treat

  /METHOD = SSTYPE(1)

  /INTERCEPT = INCLUDE

  /EMMEANS = TABLES(treat) COMPARE ADJ(LSD)

  /EMMEANS = TABLES(residual) COMPARE ADJ(LSD)

  /CRITERIA = ALPHA(.05)

  /DESIGN = units periods residual treat .

UNIANOVA

yield  BY units periods treat residual

  /METHOD = SSTYPE(1)

  /INTERCEPT = INCLUDE

  /EMMEANS = TABLES(treat) COMPARE ADJ(LSD)

  /EMMEANS = TABLES(residual) COMPARE ADJ(LSD)

  /CRITERIA = ALPHA(.05)

  /DESIGN = units periods treat residual .