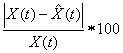Design Resources Server

Analysis of Data from Designed Experiments

Non-Linear Models
IASRI
Home

<<Back

Analysis Using SPSS

Analysis Using SAS

 

NOTE: Description of Nonlinear Models and Percentage Forecast Error

 

The mathematical representation of the nonlinear models mentioned in the problem is as follows

 

1. Logistic model is given by X(t)=c/(1+b*exp(-a*t)) + e(t) ,

 

2. Gompertz Model is represented by X(t) = c*exp(-b*exp(-a*t)) + e(t),

 

3. Monomolecular model is given by X(t) = c-(c-b)*exp(-a*t) + e(t),

 

where X(t) denotes the variable under study  at time t, ‘a’ denote the intrinsic growth rate, ‘c’ the carrying capacity of the environment,  b = [b-X(0)]/X(0) and X(0) is the value of X(t) at t = 0 and e(t) is the error term. In general the parameter ‘a’ is the coefficient of external influence emanating from the outside system.

 

One Step Ahead Forecast (OSAF)

 

In OSAF method the last observation is not considered and the model is fitted to the data set. The last value is predicted from the model and is compared with the actual value. The percentage forecast error (PCFE) is defined as

     PCFE =

where X(t) is the observed value and is the predicted value. The smaller the value of PCFE, the better fit is the model.

 

 

Refrence:

 

Draper,N.R. and Smith,H.(2005). Applied regression analysis, 3rd ed. John Wiley and Sons, New York .

Seber,G.A.F and Wild,C.J.(2003). Nonlinear regression. John-Wiley & sons. New York .

Das,P.K.(1995). Nonlinear models for studying acreage, production and productivity of wheat in India . Unpublished Ph.D. thesis, IARI, New Delhi .

Ratkowsky, D.A. (1990). Handbook of nonlinear regression models. Marcel Dekker, New York .

Ronald,G.A.(1987). Nonlinear statistical models. John Wiley and sons, New York .

Dr.Prajneshu. Lecture note on nonlinear statistical models and their applications to crops , pests and fisheries. Emanual. IASRI. New Delhi.

 

 

 

/*This SAS Code is developed at IASRI, New Delhi by Rajender Parsad, C. G. Joshy and V.K. Gupta in June 2009.

If this code is used, please quote as Rajender Parsad, V.K. Gupta and C. G. Joshy(2009).

SAS Code for Non-Linear Models available at the Link Analysis of Data at Design Resources Server.

Indian Agricultural Statistics Research Institute(ICAR), New Delhi 110 012, India.

www.iasri.res.in/design (accessed lastly on <date>).*/

The questions can be answered using the following steps.

 

Data Input:

 

For Fitting nonlinear models input the data in the following format.

{Here year is considered as independent variable and area and production (pdn) are considered as dependent variables. It may, however, be noted that one can retain the same name or can code in any other fashion.}

 

data coc;

input year  area  pdn;

datalines;

1          651370            3008

2          666618            3006

3          674378            3184

4          682281            2602

5          687483            3453

6          704682            3377

7          706107            3173

8          775600            3346

9          816900            4215

10        832200            4358

11        870000            4232

12        863100            4641

13        877000            5124

14        882300            5192

15        911000            5336

16        914300            5155

17        902100            5276

18        884300            5210

19        882300            5132

20        925035            5680

21        925783            5536

22        905718            5479

23        899198            5706

24        898498            5876

25        898200            5727

26        898000            6326

;

 

Code for Drawing Scatter Plots

 

To draw scatter plots of area and production versus time i.e., code for plotting dependent variable versus explanatory variable is as follows.

 

Note: Perform proc sql first to obtain the minimum and maximum value of each variable and these values will be used later in axis definition.

 

/*Proc sql is used to obtain the maximum and minimum values of  each variable and to form macro variables for each variable*/ 

proc sql noprint;

select max(year),min(year),max(area),min(area),max(pdn),min(pdn)into

:maxyear,  :minyear, :maxarea,:minarea ,:maxpdn,:minpdn

from coc;

/*Define the name of the variables depending upon the variables given in input statement*/

quit;

 

/*To print the assigned value of macro variables in the log window*/

%put maxyear=&maxyear,minyear=&minyear,maxarea=&maxarea,minarea=&minarea, maxpdn=&maxpdn,minpdn=&minpdn;

 

/* Create axis definitions */

/* Use the macro variables in the ORDER= option  */

axis1 order=(&minyear to &maxyear  by 1);          /* 1unit=1year*/

axis2 order=(&minarea to &maxarea  by 12000);  /*1unit=12000ha*/

axis3 order=(&minpdn to &maxpdn by 200);        /*1unit=200mn*/

 

/* Produce the plot area versus year */

/*Define data set name, xvariable, yvariable, haxis, vaxis in %macro gplot1*/

%macro gplot1(dataname=coc,xvar=year,yvar=area,haxis=axis1,vaxis=axis2);

title'Area under Coconut';

symbol color=red

        interpol=join

        value=dot

        height=.5;

        label area='area(ha)';

plot &yvar*&xvar/  haxis=&haxis vaxis=&vaxis;

run;

%mend gplot1;

 

%gplot1 /*To invoke the macro*/

run;

 

/* Produce the plot production versus year */

/*Define  data set name, xvariable, yvariable, haxis, vaxis in %macro gplot2*/

%macro gplot2(dataname=coc,xvar=year,yvar=pdn,haxis=axis1,vaxis=axis3);

proc gplot data=&dataname;

title'Production of Coconut';

symbol color=red

        interpol=join

        value=dot

        height=.5;

        label pdn='pdn(mn)';

plot &yvar*&xvar/  haxis=&haxis vaxis=&vaxis;

run;

%mend gplot2;

 

%gplot12 /*To invoke the macro*/

run;

 

Note: Data is used for illustration and not for providing projections.

 

DIFFERENT NONLINEAR MODELS FOR AREA UNDER COCONUT

 

  1. Fitting Logistic Model for Area Under Coconut

 

/*To fit the Logistic model for area under coconut*/

/*User has to define the initial parametric values(in parms) and the number of observations

(in obs=) to be used for analysis*/

proc nlin data=coc(obs=25) method=marquardt;

parms c=965569 b=25.35 a=.0874;

model area =c/(1+b*exp(-a*year));

output out=c1  sse=sse p=predict r=resid PARMS= c b a;/*To  save

error sum of squares, predicted, residual and parametric values in c1*/

run;

 

NOTE :{ The methods for obtaining initial parameter values for Logistic, Gompertz and Monomolecular model are same. Logistic model is given by the following equation

X(t) = c/(1+b*exp(-a*t)), ------(1), where b= [c-X(0)]/X(0) and X(0) is the value X(t) at t=0. The value of ‘c’ is  obtained from the plot X(t) versus t through visual examination and denote the value of ‘c’ as ‘c0’, then value of b as b0 = [c0-X(0)]/X(0)

Rearranging eq. (1) we get Z0 = ln{[c0/X(t) -1]/b0} = - At ----------(2)                    

This is a linear equation in parameter A. Now we can apply linear regression to the eq. 2, i.e. Z0 on t and obtain the estimate of A as a0. Hence, we have obtained the initial values of the three parameters a, b and c as a0, b0 and c0 respectively.

 

Draper,N.R. and Smith,H.(2005). Applied regression analysis, 3rd ed. John Wiley and Sons, New York .

Seber,G.A.F and Wild,C.J.(2003). Nonlinear regression John-Wiley & sons. New York .

Das,P.K.(1995). Nonlinear models for studying acreage, production and productivity of wheat in India . Unpublished Ph.D. thesis, IARI, New Delhi .

Ratkowsky, D.A. (1990). Handbook of nonlinear regression models. Marcel Dekker, New York .

Dr.Prajneshu. Lecture note on nonlinear statistical models and their applications to crops , pests and fisheries. Emanual. IASRI. New Delhi.

 

 

 

Code for Getting R2

/* PROC MEANS used to save the standard error and corrected sum of squares in c2*/

proc means data=coc print css stderr;

   var area;

   output out=c2 stderr=stderr css=css;

   run;

/* To produce the R-square value*/

data _null_;

   set c1(obs=1); set c2(obs=1);

   rsq = 1 - sse/css;

   file print;

      put // +10 'R-square for the non-linear model is defined' /

          +10 'as 1 - SSE/CSS, where sse is the error sum of squares of' /

          +10 'of the full model, CSS is the corrected sum of squares of'/

          +10 'the mean model. ' //

          +10 'R-square =' +5 rsq 8.6;

   run;

 

Code for Predicting the Dependent Variable (area) for the Year 2005-2006

 

/*  To predict the value of  Area */

data _null_1;

set c1(obs=1 keep=c b a);

areapred=c/(1+b*exp(-a*26)); /*Input the value of independent variable*/

file print;

put 'predicted value of area under coconut for the year 2005-2006='areapred;

run;

 

Code for Getting Percentage Forecast Error

 

/* To Calculate the vale of PCFE*/

data _null_2;

set _null_1;

PCFE=abs(((898000-areapred)/898000)*100); /*Input the value of dependent variable*/

file print;

put 'OSAF='PCFE;

run;

 

2. Fitting Monomolecular Model for Area Under Coconut

 

/*To fit the Monomolecular model for area under coconut*/

/*User has to define the initial parametric values(in parms) and the number of observations

(in obs=) to be used for analysis*/

proc nlin data=coc(obs=25) method=marquardt;

parms c=965569 b=25.35 a=.0874;

model area =c-((c-b)*exp(-a*year));

output out=c1  sse=sse p=predict r=resid PARMS= c b a;/*To  save

error sum of squares, predicted, residual and parametric values in c1*/

run;

 

Code for Getting R2

 

/* PROC MEANS used to save the standard error and corrected sum of squares in c2*/

proc means data=coc print css stderr;

   var area;

   output out=c2 stderr=stderr css=css;

   run;

/* To produce the R-square value*/

data _null_;

   set c1(obs=1); set c2(obs=1);

   rsq = 1 - sse/css;

   file print;

   put // +10 'R-square for the non-linear model is defined' /

          +10 'as 1 - SSE/CSS, where sse is the error sum of squares of' /

          +10 'of the full model, CSS is the corrected sum of squares of'/

          +10 'the mean model. ' //

          +10 'R-square =' +5 rsq 8.6;

   run;

 

Code for Predicting the Dependent Variable (area) for the Year 2005-2006

 

/* To predict the value of Area */

data _null_1;

set c1(obs=1 keep=c b a);

areapred=c-((c-b)*exp(-a*26)); /*Input the value of independent variable*/

file print;

put 'predicted value of area for the year 2005-2006='areapred;

run;

 

Code for Getting Percentage Forecast Error

 

/* To Calculate the vale of PCFE*/

data _null_2;

set _null_1;

PCFE=abs(((898000-areapred)/898000)*100); /*Input the value of dependent variable*/

file print;

put 'OSAF='PCFE;

run;

 

 3. Fitting Gompertz Model for Area Under Coconut

 

/*To fit the Gompertz model for area under coconut*/

/*User has to define the initial parametric values(in parms) and the number of observations

(in obs=) to be used for analysis*/

proc nlin data=coc(obs=25) method=marquardt;

parms c=965569 b=25.35 a=.0874;

model area =c*exp(-b*exp(-a*year));

output out=c1  sse=sse p=predict r=resid PARMS= c b a;/*To  save

error sum of squares, predicted, residual and parametric values in c1*/

run;

Code for Getting R2

 

/* PROC MEANS used to save the standard error and corrected sum of squares in c2*/

proc means data=coc print css stderr;

   var area;

   output out=c2 stderr=stderr css=css;

   run;

/* To produce the R-square value*/

data _null_;

   set c1(obs=1); set c2(obs=1);

   rsq = 1 - sse/css;

   file print;

   put // +10 'R-square for the non-linear model is defined' /

          +10 'as 1 - SSE/CSS, where sse is the error sum of squares of' /

          +10 'of the full model, CSS is the corrected sum of squares of'/

          +10 'the mean model. ' //

          +10 'R-square =' +5 rsq 8.6;

   run;

 

Code for Predicting the Dependent Variable (area) for the Year 2005-2006

 

/* To predict the value of Area */

data _null_1;

set c1(obs=1 keep=c b a);

areapred=c*exp(-b*exp(-a*26)); /*Input the value of independent variable*/

file print;

put 'predicted value of area for the year 2005-2006='areapred;

run;

 

Code for Getting Percentage Forecast Error

 

/* To Calculate the vale of PCFE*/

data _null_2;

set _null_1;

PCFE=abs(((898000-areapred)/898000)*100); /*Input the value of dependent variable*/

file print;

put 'OSAF='PCFE;

run;

 

DIFFERENT NONLINEAR MODELS FOR PRODUCTION OF COCONUT

 

1. Fitting Logistic Model for Production of Coconut

 

/* To fit the Logistic model for production of coconut*/

/*User has to define the initial parametric values(in parms) and the number of observations

(in obs=) to be used for analysis*/

proc nlin data=coc (obs=25) method=marquardt ;

parms c=5876 b=1.133 a=.01354;

model pdn =c/(1+b*exp(-a*year));

output out=c1  sse=sse p=predict r=resid PARMS= c b a;/*To  save

error sum of squares, predicted, residual and parametric values in c1*/

run;

 

Code for Getting R2

 

/* PROC MEANS used to save the standard error and corrected sum of squares in c2*/

proc means data=coc print css stderr;

   var pdn;

   output out=c2 stderr=stderr css=css;

   run;

/* To produce the R-square value*/

data _null_;

   set c1(obs=1); set c2(obs=1);

   rsq = 1 - sse/css;

   file print;

   put // +10 'R-square for the non-linear model is defined' /

          +10 'as 1 - SSE/CSS, where sse is the variance of' /

          +10 'of the full model, CSS is the variance of   ' /

          +10 'the mean model. ' //

          +10 'R-square =' +5 rsq 8.6; /*+5 rsq 8.6:- it leaves 5 columns after the equal to sign and there are total eight digits including decimal point in the R-square value such that one digit before the decimal point and 6 digits after the decimal point*/

   run;

 

Code for Predicting the Dependent Variable (pdn) for the Year 2005-2006

 

/* To predict the value of Production */

data _null_1;

set c1(obs=1 keep=c b a);

pdnpred=c/(1+b*exp(-a*26)); /*Input the value of independent variable*/

file print;

put 'predicted value of production of coconut for the year 2005-2006='pdnpred;

run;

 

Code for Getting Percentage Forecast Error

 

/* To Calculate the vale of PCFE*/

data _null_2;

set _null_1;

PCFE=abs(((6326-pdnpred)/6326)*100); /*Input the value of dependent variable*/

file print;

put 'OSAF='PCFE;

run;

 

2. Fitting Monomolecular Model for Production of Coconut

 

/* To fit the Monommolecular model for production of coconut*/

/*User has to define the initial parametric values(in parms) and the number of observations

(in obs=) to be used for analysis*/

proc nlin data=coc (obs=25) method=marquardt ;

parms c=5876 b=1.133 a=.01354;

model pdn =c-(c-b)*exp(-a*year);

output out=c1  sse=sse p=predict r=resid PARMS= c b a;/*To  save

error sum of squares, predicted, residual and parametric values in c1*/

run;

Code for Getting R2

 

/* PROC MEANS used to save the standard error and corrected sum of squares in c2*/

proc means data=coc print css stderr;

   var pdn;

   output out=c2 stderr=stderr css=css;

   run;

/* To produce the R-square value*/

data _null_;

   set c1(obs=1); set c2(obs=1);

   rsq = 1 - sse/css;

   file print;

   put // +10 'R-square for the non-linear model is defined' /

          +10 'as 1 - SSE/CSS, where sse is the variance of' /

          +10 'of the full model, CSS is the variance of   ' /

          +10 'the mean model. ' //

          +10 'R-square =' +5 rsq 8.6;  /*+5 rsq 8.6:- it leaves 5 columns after the equal to sign and there are total eight digits including decimal point in the R-square value such that one digit before the decimal point and 6 digits after the decimal point*/

   run;

 

Code for Predicting the Dependent Variable (pdn) for the Year 2005-2006

 

/* To predict the value of Production */

data _null_1;

set c1(obs=1 keep=c b a);

pdnpred=c-(c-b)*exp(-a*26); /*Input the value of independent variable*/

file print;

put 'predicted value of production of coconut for the year 2005-2006='pdnpred;

run;

 

Code for Getting Percentage Forecast Error

 

/* To Calculate the vale of PCFE*/

data _null_2;

set _null_1;

PCFE=abs(((6326-pdnpred)/6326)*100); /*Input the value of dependent variable*/

file print;

put 'OSAF='PCFE;

run;

 

 

3. Gompertz Model for Production of Coconut

 

/* To fit the Gompertz model for production of coconut*/

/*User has to define the initial parametric values(in parms) and the number of observations

(in obs=) to be used for analysis*/

proc nlin data=coc (obs=25) method=marquardt ;

parms c=5876 b=1.133 a=.01354;

model pdn =c*exp(-b*exp(-a*year));

output out=c1  sse=sse p=predict r=resid PARMS= c b a;/*To  save

error sum of squares, predicted, residual and parametric values in c1*/

run;

 

Code for Getting R2

 

/* PROC MEANS used to save the standard error and corrected sum of squares in c2*/

proc means data=coc print css stderr;

   var pdn;

   output out=c2 stderr=stderr css=css;

   run;

/* To produce the R-square value*/

data _null_;

   set c1(obs=1); set c2(obs=1);

   rsq = 1 - sse/css;

   file print;

   put // +10 'R-square for the non-linear model is defined' /

          +10 'as 1 - SSE/CSS, where sse is the variance of' /

          +10 'of the full model, CSS is the variance of   ' /

          +10 'the mean model. ' //

          +10 'R-square =' +5 rsq 8.6; /*+5 rsq 8.6:- it leaves 5 columns after the equal to sign and there are total eight digits including decimal point in the R-square value such that one digit before the decimal point and 6 digits after the decimal point*/

   run;

 

Code for Predicting the Dependent Variable (pdn) for the Year 2005-2006

 

/* To predict the value of Production */

data _null_1;

set c1(obs=1 keep=c b a);

pdnpred=c*exp(-b*exp(-a*26)); /*Input the value of independent variable*/

file print;

put 'predicted value of production of coconut for the year 2005-2006='pdnpred;

run;

 

Code for Getting Percentage Forecast Error

 

/* To Calculate the vale of PCFE*/

data _null_2;

set _null_1;

PCFE=abs(((6326-pdnpred)/6326)*100); /*Input the value of dependent variable*/

 

file print;

put 'OSAF='PCFE;

run;

 

 

Data File

Result File  

 <<Back

 Analysis Using SAS                                                         Analysis Using SPSS                                     

 

 

 

Home Descriptive Statistics  Tests of Significance Correlation and Regression Completely Randomised Design  RCB Design  

Incomplete Block Design  Resolvable Block Design  Augmented Design  Latin Square Design Factorial RCB Design  

Partially Confounded Design Factorial Experiment with Extra Treatments Split Plot Design Strip Plot Design 

Response Surface Design Cross Over Design  Analysis of Covariance Diagnostics and Remedial Measures 

Principal Component Analysis Cluster Analysis Groups of Experiments  Non-Linear Models  

Contact Us 

 

 

 

 

  Copyright        Disclaimer        How to Quote this page        Report Error        Comments/suggestions

Descriptive Statistics
Tests of Significance
Correlation and Regression
Completely Randomised Design
RCB Design
Incomplete Block Design
Resolvable Block Design
Augmented Design
Latin Square Design
Factorial RCB Design
Partially Confounded Design
Factorial Experiment with Extra Treatments
Split Plot Design
Strip Plot Design
Response Surface Design
Cross-Over Designs
Analysis of Covariance
Diagnostics and Remedial Measures
Principal Component Analysis
Cluster Analysis
Groups of Experiments
Non-Linear Models
Contact Us

Other Designed Experiments
     (Under Development)

For exposure on SAS, SPSS, 
MINITAB, SYSTAT and  
MS-EXCEL for analysis of data from designed experiments:

 Please see Module I of Electronic Book II:
Advances in Data Analytical Techniques

available at Design Resources Server (www.iasri.res.in/design)