 |
Analysis of Data from Designed Experiments |
 |
|
Balanced Confounded Factorial Experiment with Extra Treatment |
Analysis Using SAS
Analysis Using SPSS
Main
Procedure is:
Start
→All Programs → SPSS for Windows →
SPSS 15.0/ SPSS13.0/ SPSS10.0 (based on the version
available on your machine) → Enter data in Data
Editor → Analyze → GLM →
Univariate → yield → [puts
yield under Dependent list:] → block
→ [puts block under Fixed Factor(s):
] trt → [puts trt under
Fixed Factor(s):] rep → [puts rep under
Fixed Factor(s):]Continue → Model... [Opens
Model dialogue box] → Custom → Build
Term(s) → Main effects →
[puts rep, block, trt under Model: ] →
Paste → It comes in Syntax mode, then define
model as rep block(rep) trt → Run All.
To test the significance of
19 treatment combinations and identify the best treatment
combination and to compare all the 18 treatment combinations
with the control treatment requires analysis to be performed
on treatment combinations. Therefore, 19 treatment
combinations are recoded as:
|
N
|
P
|
K
|
Treatment |
|
40 |
0 |
0 |
1 |
|
40 |
0 |
40 |
2 |
|
40 |
40 |
0 |
3 |
|
40 |
40 |
40 |
4 |
|
40 |
80 |
0 |
5 |
|
40 |
80 |
40 |
6 |
|
80 |
0 |
0 |
7 |
|
80 |
0 |
40 |
8 |
|
80 |
40 |
0 |
9 |
|
80 |
40 |
40 |
10 |
|
80 |
80 |
0 |
11 |
|
80 |
80 |
40 |
12 |
|
120 |
0 |
0 |
13 |
|
120 |
0 |
40 |
14 |
|
120 |
40 |
0 |
15 |
|
120 |
40 |
40 |
16 |
|
120 |
80 |
0 |
17 |
|
120 |
80 |
40 |
18 |
|
0 |
0 |
0 |
19 |
Using
the procedure of block design with factorial structure, the contrasts for main effects and interactions are:|
N: |
1 |
1 |
1 |
1 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
0 |
|
|
P: |
1 |
1 |
-1 |
-1 |
0 |
0 |
1 |
1 |
-1 |
-1 |
0 |
0 |
1 |
1 |
-1 |
-1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
-2 |
-2 |
1 |
1 |
1 |
1 |
-2 |
-2 |
1 |
1 |
1 |
1 |
-2 |
-2 |
0 |
|
|
K: |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
0 |
|
NP: |
1 |
1 |
-1 |
-1 |
0 |
0 |
-1 |
-1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
-2 |
-2 |
-1 |
-1 |
-1 |
-1 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
1 |
1 |
-1 |
-1 |
0 |
0 |
1 |
1 |
-1 |
-1 |
0 |
0 |
-2 |
-2 |
2 |
2 |
0 |
0 |
0 |
|
|
1 |
1 |
1 |
1 |
-2 |
-2 |
1 |
1 |
1 |
1 |
-2 |
-2 |
-2 |
-2 |
-2 |
-2 |
4 |
4 |
0 |
|
|
NK: |
1 |
-1 |
1 |
-1 |
1 |
-1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
-2 |
2 |
-2 |
2 |
-2 |
2 |
0 |
|
|
PK: |
1 |
-1 |
-1 |
1 |
0 |
0 |
1 |
-1 |
-1 |
1 |
0 |
0 |
1 |
-1 |
-1 |
1 |
0 |
0 |
0 |
|
1 |
-1 |
1 |
-1 |
-2 |
2 |
1 |
-1 |
1 |
-1 |
-2 |
2 |
1 |
-1 |
1 |
-1 |
-2 |
2 |
0 |
|
|
NPK: |
1 |
-1 |
-1 |
1 |
0 |
0 |
-1 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
-1 |
1 |
-1 |
-2 |
2 |
-1 |
1 |
-1 |
1 |
2 |
-2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
1 |
-1 |
-1 |
1 |
0 |
0 |
1 |
-1 |
-1 |
1 |
0 |
0 |
-2 |
2 |
2 |
-2 |
0 |
0 |
0 |
|
|
1 |
-1 |
1 |
-1 |
-2 |
2 |
1 |
-1 |
1 |
-1 |
-2 |
2 |
-2 |
2 |
-2 |
2 |
4 |
-4 |
0 |
|
|
Control
vs rest |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
-18 |
For
performing analysis, input the data in the following format.
{Here
the replication is termed as rep, treatment as trt and the
three factors as N, P and K. It may however, be noted
that one can retain the same name or can code in any other
fashion}.
Following
are the brief description of the steps along with screen
shots.
· Open Data editor: Start → All Programs → SPSS for Windows → SPSS 15.0/ SPSS13.0/ SPSS10.0
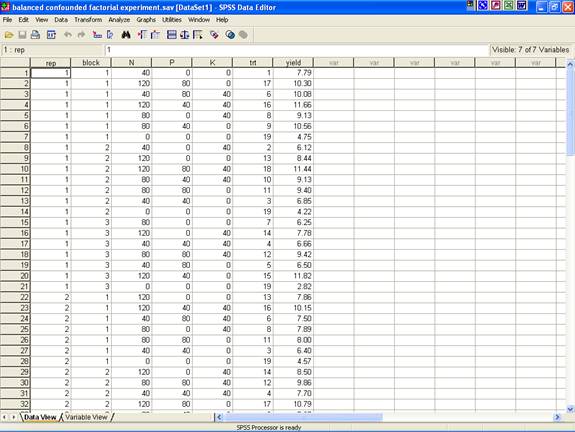
· Enter data in SPSS Data Editor. There are two views in SPSS Data Editor. In variable view, one can define the name of variables and variable types string or numeric and data view gives the spreadsheet in which data pertaining to variables may be entered in respective columns. In the present case, we enter data in numeric format.
· Once the data entry is complete, Choose Analyze from the Menu Bar. Now select Analyze → General linear Model → Univariate.
· This selection displays the following screen.
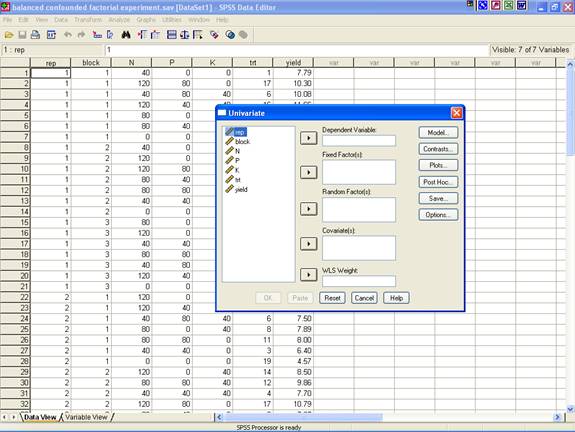
· Select yield and send it to the Dependent Variable box; rep, block and trt may be selected for Fixed Factor(s) box. After doing these the dialog box should be like this
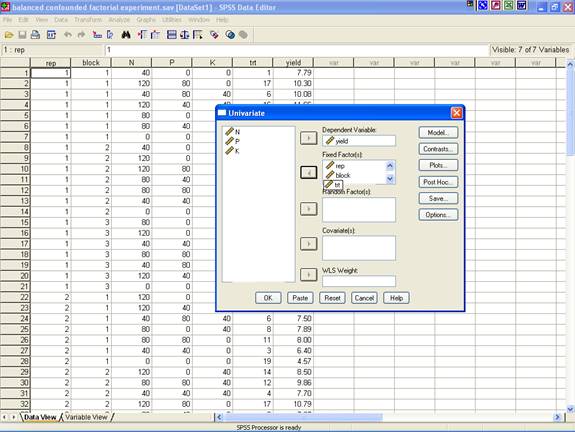
·
Select Model in
the Univariate dialog box i.e. → Model... [Opens
Model dialogue box]. Put rep, block and trt under
the model for main effects
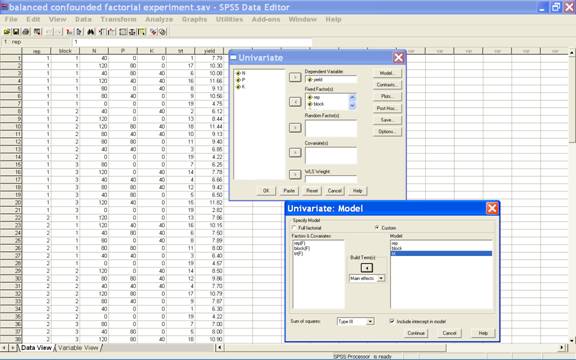
·
Click Continue
to return to the Univariate dialog box.
·
All
possible pair wise treatment comparisons can be performed
using the Button Options on the dialogue box. A click
on Button Options, gives the option for estimated marginal
means and display means for. From the left hand box, take
the effect treatment in the Display means for. Then
check the box Compare main effects and then there are 3
options for confidence interval adjustment viz.
LSD(none), Bonferrnoni and Sidak. Any one of these 3 options
can be selected. Default option is LSD(None).
A screen shot for these options is
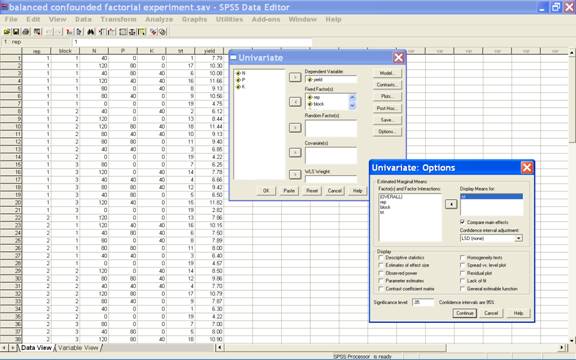
·
Click Continue
to return to the Univariate dialog box.
Click
Paste to get the commands in syntax editor. Now
define model as per design adopted to analyze the data. Here
it is
/Design
= rep block(rep) trt.
i)
For testing the significance of the main effects and also
the interaction effects and
ii)
For testing whether the average of all the 18 treatment
combinations is significantly different from control
treatment
One
can use the following statements
/Lmatrix
'N' trt 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 0 0 0 0 0 0 0;
trt 1 1 1 1 1 1 1 1 1 1 1 1 -2 -2 -2 -2 -2 -2 0;
/Lmatrix
'P' trt 1 1 -1 -1 0 0 1 1 -1 -1 0 0 1 1 -1 -1 0 0 0;
trt 1 1 1 1 -2 -2 1 1 1 1 -2 -2 1 1 1 1 -2 -2 0;
/Lmatrix
'K' trt 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 0;
/Lmatrix
‘NP’ trt 1 1 -1 -1 0 0 -1 -1 1 1 0 0 0 0 0 0 0 0 0;
trt 1 1 1 1 -2 -2 -1 -1 -1 -1 2 2 0 0 0 0 0 0 0;
trt 1 1 -1 -1 0 0 1 1 -1 -1 0 0 -2 -2 2 2 0 0 0;
trt 1 1 1 1 -2 -2 1 1 1 1 -2 -2 -2 -2 -2 -2 4 4 0;
/Lmatrix
‘NK’ trt 1 -1 1 -1 1 -1 -1 1 -1 1 -1 1 0 0 0 0 0 0 0;
trt 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 -2 2 -2 2 -2 2 0;
/Lmatrix
'PK' trt 1 -1 -1 1 0 0 1 -1 -1 1 0 0 1 -1 -1 1 0 0 0;
trt 1 -1 1 -1 -2 2 1 -1 1 -1 -2 2 1 -1 1 -1 -2 2 0;
/Lmatrix
‘NPK’ trt 1 -1 -1 1 0 0 -1 1 1 -1 0 0 0 0 0 0 0 0 0;
trt 1 -1 1 -1 -2 2 -1 1 -1 1 2 -2 0 0 0 0 0 0 0;
trt 1 -1 -1 1 0 0 1 -1 -1 1 0 0 -2 2 2 -2 0 0 0;
trt 1 -1 1 -1 -2 2 1 -1 1 -1 -2 2 -2 2 -2 2 4 -4 0;
/Lmatrix ‘Control vs rest' trt 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 -18;
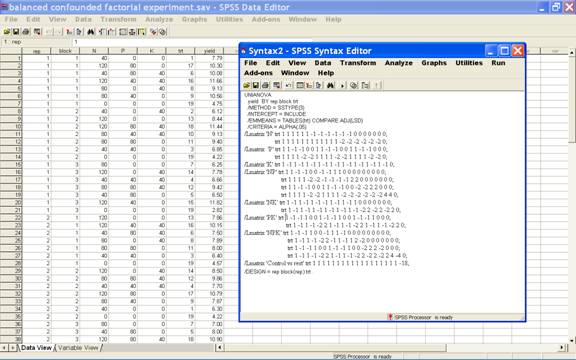
·
Click Run
→ All.
To
answer all the questions 1 to 3, the following syntax may be
used after creating the data file.
UNIANOVA
yield BY
rep block trt
/METHOD = SSTYPE(3)
/INTERCEPT = INCLUDE
/EMMEANS = TABLES(trt) COMPARE ADJ(LSD)
/CRITERIA = ALPHA(.05)
/Lmatrix
'N' trt 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 0 0 0 0 0 0 0;
trt 1 1 1 1 1 1 1 1 1 1 1 1 -2 -2 -2 -2 -2 -2 0;
/Lmatrix
'P' trt 1 1 -1 -1 0 0 1 1 -1 -1 0 0 1 1 -1 -1 0 0 0;
trt 1 1 1 1 -2 -2 1 1 1 1 -2 -2 1 1 1 1 -2 -2 0;
/Lmatrix
'K' trt 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 0;
/Lmatrix
'NP' trt 1 1 -1 -1 0 0 -1 -1 1 1 0 0 0 0 0 0 0 0 0;
trt 1 1 1 1 -2 -2 -1 -1 -1 -1 2 2 0 0 0 0 0 0 0;
trt 1 1 -1 -1 0 0 1 1 -1 -1 0 0 -2 -2 2 2 0 0 0;
trt 1 1 1 1 -2 -2 1 1 1 1 -2 -2 -2 -2 -2 -2 4 4 0;
/Lmatrix
'NK' trt 1 -1 1 -1 1 -1 -1 1 -1 1 -1 1 0 0 0 0 0 0 0;
trt 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 -2 2 -2 2 -2 2 0;
/Lmatrix
'PK' trt 1 -1 -1 1 0 0 1 -1 -1 1 0 0 1 -1 -1 1 0 0 0;
trt 1 -1 1 -1 -2 2 1 -1 1 -1 -2 2 1 -1 1 -1 -2 2 0;
/Lmatrix
'NPK' trt 1 -1 -1 1 0 0 -1 1 1 -1 0 0 0 0 0 0 0 0 0;
trt 1 -1 1 -1 -2 2 -1 1 -1 1 2 -2 0 0 0 0 0 0 0;
trt 1 -1 -1 1 0 0 1 -1 -1 1 0 0 -2 2 2 -2 0 0 0;
trt 1 -1 1 -1 -2 2 1 -1 1 -1 -2 2 -2 2 -2 2 4 -4 0;
/Lmatrix
'Control vs rest' trt 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
-18;
/DESIGN
= rep block(rep)
trt .
Analysis Using SAS Analysis Using SPSS
Home Descriptive Statistics Tests of Significance Correlation and Regression Completely Randomised Design RCB Design
Incomplete Block Design Resolvable Block Design Augmented Design Latin Square Design Factorial RCB Design
Partially Confounded Design Factorial Experiment with Extra Treatments Split Plot Design Strip Plot Design
Response Surface Design Cross Over Design Analysis of Covariance Diagnostics and Remedial Measures
Principal Component Analysis Cluster Analysis Groups of Experiments Non-Linear Models
Copyright Disclaimer How to Quote this page Report Error Comments/suggestions
(Under Development)
For exposure on SAS, SPSS,
MINITAB, SYSTAT and
MS-EXCEL for analysis of
data from designed experiments:
Please see Module I of Electronic Book II: Advances in Data Analytical Techniques
available at Design Resource Server (www.iasri.res.in/design)